ランチタイムのお供に
数分でできる一問をランチタイムのお供にいかがですか?
出典がどこかに行ってしまったのですが、
多分、どこかの入試問題だと思います。
まぁ、小問集合の中の一問でしょうねぇ・・・。
では、問題です。
整式$x^{25}-x^{13}+5$を,$(x+1)^2$で割ったときのあまりを求めよ。
コレです。シンプルな計算問題です。
まずは方針を決めてください。
(0) 実際に割り算
ーーーーーーー
まずは,除法の原理で($Q(x)$:整式,$a,\,b$:実数として)
$f(x)=x^{25}-x^{13}+5=(x+1)^2\cdot Q(x)+ax+b$ などと表したあとに,
(1) あまりの変形
(2) 数値代入で押し切る
(3) 微分
・ (スクロールすると方針に関するヒントが現れます)
・
・
・
・
・
・
・
・
・
正解に至る方針は2つです。
(0) か (3)
(0)でやると・・・
6年ぐらい前に、授業中に「実際に割ってもできますよ~」と言ってしまったのが運の尽き・・・
「じゃぁやってみせてください!!」と言われてしまい、やったのが次の写真です。

筆算するときの工夫!? ですが、・・・・
係数だけを拾って計算しています。
ヨコ方向の位置がズレないように,慎重にやっています。
(実際には、一箇所ぐらいズレても解答は変わらないんですけどね・・・)
また,そのまま書くとタテ方向に足りなくなるので,ずらして書いています。
(そのため、意味不明かもしれません。わからなければ質問コメント下さいね~)
皆さんは(3)でやりましょうね~。
答えは $12x+17$ です。
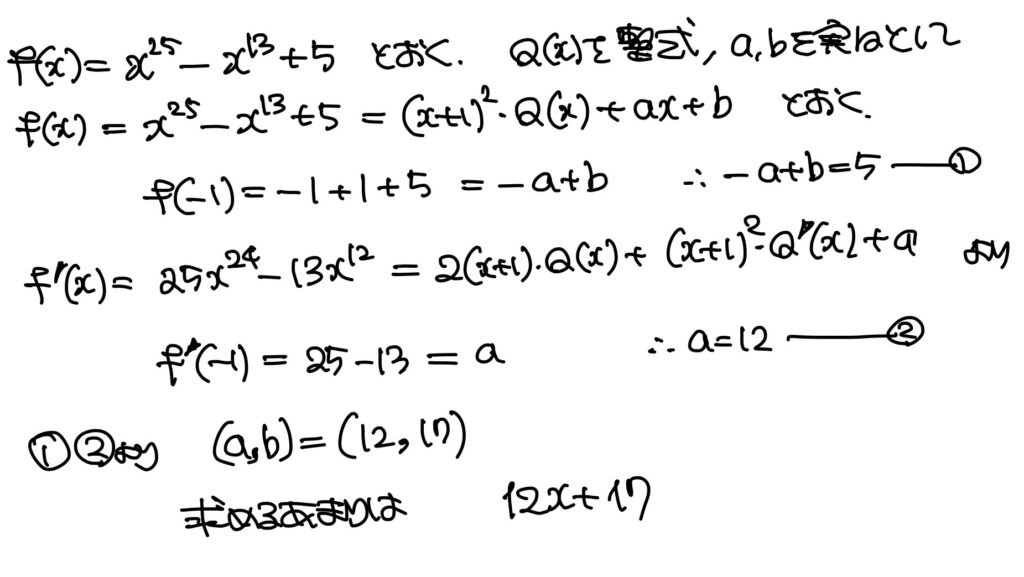


コメントを残す